-
Quantile
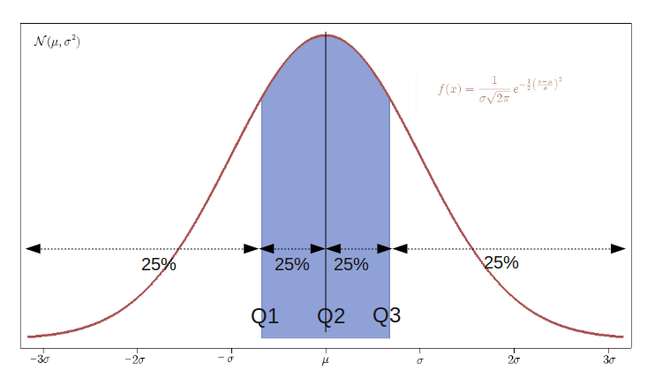
In statistics and probability quantiles are cut points dividing the range of a probability distribution into continuous intervals with equal probabilities, or dividing the observations in a sample in the same way. There is one less quantile than the number of groups created. Thus quartiles are the three cut points that will divide a dataset into four equal-sized groups. Common quantiles have special names: for instance quartile, decile (creating 10 groups: see below for more). The groups created are termed halves, thirds, quarters, etc., though sometimes the terms for the quantile are used for the groups created, rather than for the cut points.
q-quantiles are values that partition a finite set of values into q subsets of (nearly) equal sizes. There are q − 1 of the q-quantiles, one for each integer k satisfying 0
-
Fractile (noun)
The value of a distribution for which some fraction of the sample lies below.
“The q-quantile is the same as the (1/q)-fractile.”
“The median is the .5-fractile.”
-
Fractile (adjective)
Describing the quality of a sedimentary stone as it relates to the sediments to cohesively bond without fracturing.
“A stone with a low fractile strength lacks tensile strength and will crack or crumble under stress or pressure.”
-
Quantile (noun)
One of the class of values of a variate which divides the members of a batch or sample into equal-sized subgroups of adjacent values or a probability distribution into distributions of equal probability.
-
Quantile (noun)
each of any set of values of a variate which divide a frequency distribution into equal groups, each containing the same fraction of the total population.
-
Quantile (noun)
any of the groups so produced, e.g. a quartile or percentile.