Ellipsoid vs. Ellipse

Main Difference

The main difference between Ellipsoid and Ellipse is that the Ellipsoid is a closed quadric surface that is a three dimensional analogue of an ellipse and Ellipse is a type of curve on a plane.

• Ellipsoid

  An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

  An ellipsoid is a quadric surface;  that is, a surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, an ellipsoid is characterized by either of the two following properties. Every planar cross section is either an ellipse, or is empty, or is reduced to a single point (this explains the name, meaning “ellipse like”). It is bounded, which means that it may be enclosed in a sufficiently large sphere.

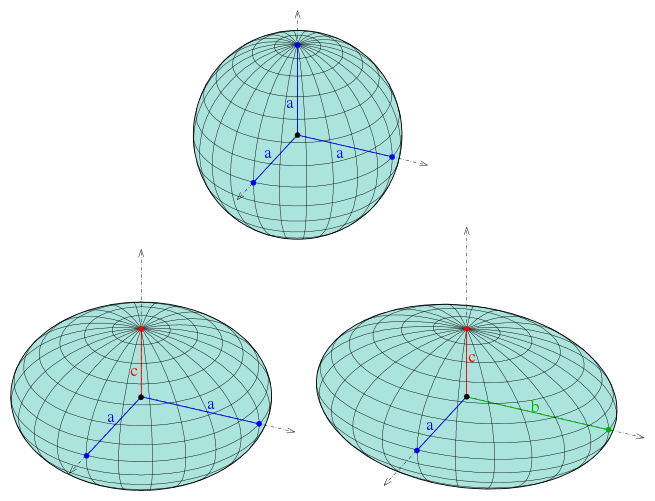
  An ellipsoid has three pairwise perpendicular axes of symmetry which intersect at a center of symmetry, called the center of the ellipsoid. The line segments that are delimited on the axes of symmetry by the ellipsoid are called the principal axes, or simply axes of the ellipsoid. If the three axes have different lengths, the ellipsoid is said to be tri-axial or rarely scalene, and the axes are uniquely defined.

  If two of the axes have the same length, then the ellipsoid is an ellipsoid of revolution, also called a spheroid. In this case, the ellipsoid is invariant under a rotation around the third axis, and there are thus infinitely many ways of choosing the two perpendicular axes of the same length. If the third axis is shorter, the ellipsoid is an oblate spheroid; if it is longer, it is a prolate spheroid. If the three axes have the same length, the ellipsoid is a sphere.

• Ellipse

  In mathematics, an ellipse is a curve in a plane surrounding two focal points such that the sum of the distances to the two focal points is constant for every point on the curve. As such, it is a generalization of a circle, which is a special type of an ellipse having both focal points at the same location. The shape of an ellipse (how “elongated” it is) is represented by its eccentricity, which for an ellipse can be any number from 0 (the limiting case of a circle) to arbitrarily close to but less than 1.

  Ellipses are the closed type of conic section: a plane curve resulting from the intersection of a cone by a plane (see figure to the right). Ellipses have many similarities with the other two forms of conic sections: parabolas and hyperbolas, both of which are open and unbounded. The cross section of a cylinder is an ellipse, unless the section is parallel to the axis of the cylinder.

  Analytically, an ellipse may also be defined as the set of points such that the ratio of the distance of each point on the curve from a given point (called a focus or focal point) to the distance from that same point on the curve to a given line (called the directrix) is a constant. This ratio is the above-mentioned eccentricity of the ellipse.

  An ellipse may also be defined analytically as the set of points for each of which the sum of its distances to two foci is a fixed number.

  Ellipses are common in physics, astronomy and engineering. For example, the orbit of each planet in our solar system is approximately an ellipse with the barycenter of the planet–Sun pair at one of the focal points. The same is true for moons orbiting planets and all other systems having two astronomical bodies. The shapes of planets and stars are often well described by ellipsoids. Ellipses also arise as images of a circle under parallel projection and the bounded cases of perspective projection, which are simply intersections of the projective cone with the plane of projection. It is also the simplest Lissajous figure formed when the horizontal and vertical motions are sinusoids with the same frequency. A similar effect leads to elliptical polarization of light in optics.

  The name, ἔλλειψις (élleipsis, “omission”), was given by Apollonius of Perga in his Conics, emphasizing the connection of the curve with “application of areas”.