-
Diameter
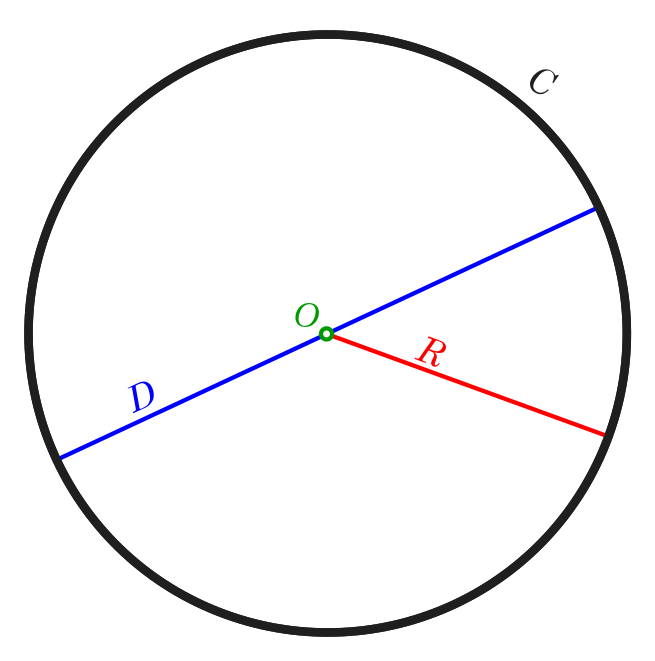
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere.
In more modern usage, the length of a diameter is also called the diameter. In this sense one speaks of the diameter rather than a diameter (which refers to the line itself), because all diameters of a circle or sphere have the same length, this being twice the radius r.
d
=
2
r
⇒
r
=
d
2
.
{displaystyle d=2rquad Rightarrow quad r={frac {d}{2}}.}
For a convex shape in the plane, the diameter is defined to be the largest distance that can be formed between two opposite parallel lines tangent to its boundary, and the width is often defined to be the smallest such distance. Both quantities can be calculated efficiently using rotating calipers. For a curve of constant width such as the Reuleaux triangle, the width and diameter are the same because all such pairs of parallel tangent lines have the same distance.
For an ellipse, the standard terminology is different. A diameter of an ellipse is any chord passing through the center of the ellipse. For example, conjugate diameters have the property that a tangent line to the ellipse at the endpoint of one of them is parallel to the other one. The longest diameter is called the major axis.
The word “diameter” is derived from Greek διάμετρος (diametros), “diameter of a circle”, from διά (dia), “across, through” and μέτρον (metron), “measure”. It is often abbreviated DIA, dia, d, or ⌀.
-
Diametre (noun)
alternative form of diameter
-
Diameter (noun)
Any straight line between two points on the circumference of a circle that passes through the centre/center of the circle.
-
Diameter (noun)
The length of such a line.
-
Diameter (noun)
The maximum distance between any two points in a metric space
-
Diameter (noun)
The maximum eccentricity over all vertices in a graph.
